In this lecture, we will introduce the idea of tree based data structure. Trees are a very common type of data structure used in CS to represent a myriad of things. Just a few examples
- A tree is what’s used to implement
TreeSetandTreeMapto keep data sorted and efficiently findable - Folders and files in a computer form a tree where there is a top folder (the root) and sub-files (children). We’ll see that just like the file was defined recursively, a tree will be defined recursively as well.
- A family tree (parents and children) to track genealogy or an organizational chart.
- And much much more!
Some Definitions
In 143, we will focus mostly on making a tree that stores int values to see how TreeSet is implemented, but almost everything we discuss here can be extended to any of the applications above.
A tree will be represented as a series of nodes linked together in some hierarchical fashion (see below). This is similar to the idea of the ListNode forming up a linked list, but these nodes may store more than one “next” reference. We call the nodes below a particular node the children of that node; conversely, we call a node above some node the parent of that node (just like a family tree!).
In this class we will focus binary trees, where every node in the tree has at most 2 children (could be 0, could be 1, or could be 2). The picture below shows a binary tree.
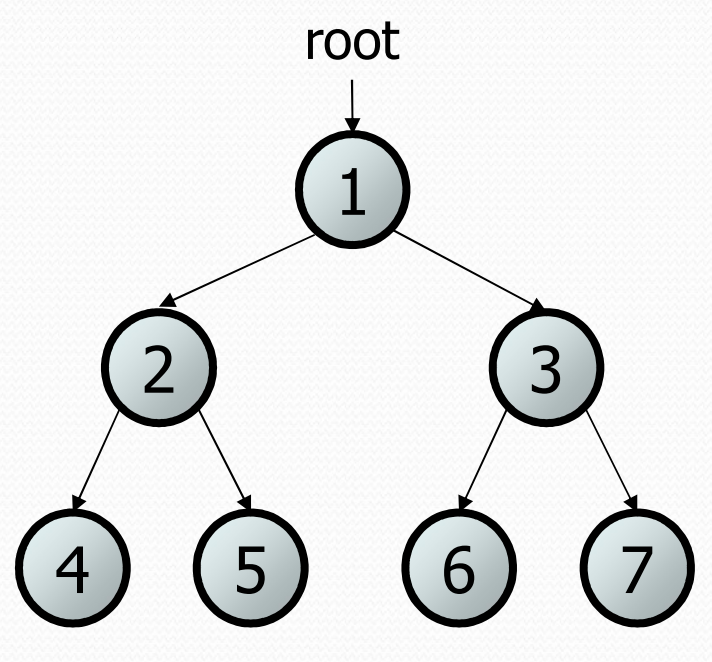
The binary tree has a very natural recursive definition that matches a tree of any height! A tree is one of two possibilities
- An empty tree (or
null) - A root node that contains:
- Some data (an
int) - A left subtree
- A right subtree
- Some data (an
These left/right subtrees also follow the definition of trees above! This means they could be empty, or they could be a node with some data and two subtree children! This definition could go on and on for as long as necessary since it is recursive.
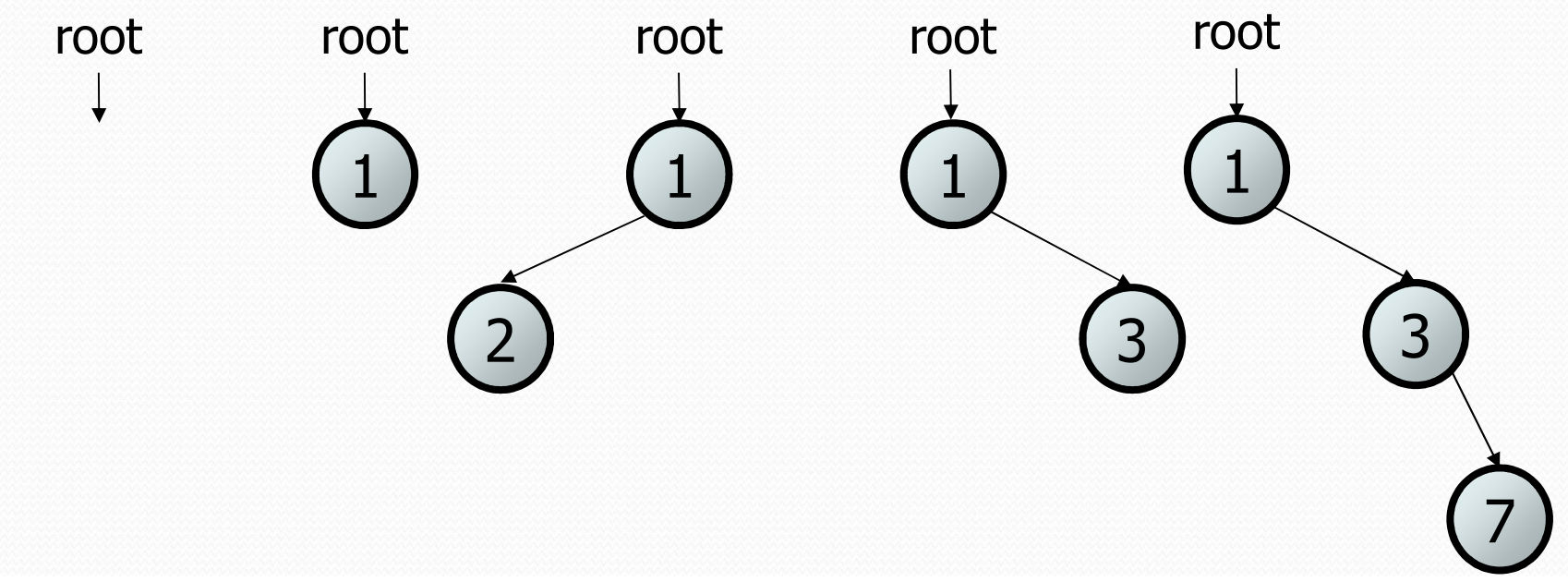
Here are some examples of binary trees (notice they all match this recursive definition since some of the subtrees are empty which is allowed!). We will start lecture on Friday discussing why these are all binary trees, so don’t worry if that doesn’t make full sense.
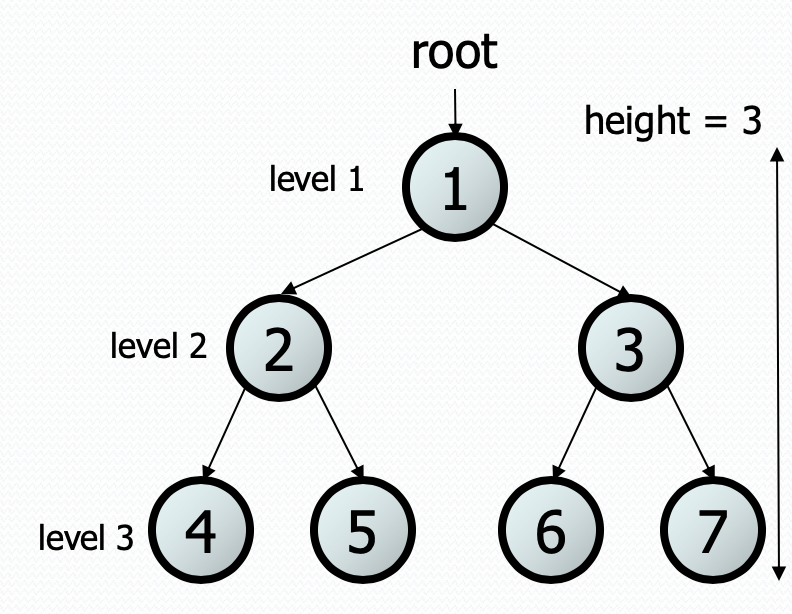
Terminology
There is usually a lot of terminology that goes along when learning trees. This section will quickly go through some definitions that are commonly used when referring to trees. Recall that this class is not a “memorize the definition” class so if a problem ever uses one of these terms, it is almost always accompanied by an example that should make it more clear if you don’t fully remember the terms.
- A node is a building block the tree that will contain some data value and its left/right subtrees.
- root: The topmost node of a tree
- leaf: A node that has no children (i.e. both children are empty trees)
- branch: An internal node; neither the root nor a leaf.
- parent of a node: A node that refers to this node (in the picture below, 1 is a parent of both 2 and 3)
- child of a node: A node that is referred to by this node (in the picture below, 2 and 3 are children of 1)
- sibling of a node: Another node in the tree with a common parent (2 and 3 are siblings in the picture below).
- subtree: The smaller tree of nodes to the left/right of the current node
- height: The length of the longest path from the root to any node (the height of the tree in the picture below is 3)
- level or depth: The length of the path from a root to a given node.